PeLU: Porcelain-Emulated Linear Unit

Saturday, December 4, 2021 · 6 min read

The other day my toilet broke and I involuntarily learned a lot about how flushing works. My friend suggested an analogy for me: flushing toilets is like a neuron’s activation: once a critical threshold is met, there’s an “all-at-once” response.

That got me thinking, could we implement deep neural networks in plumbing? It turns out, the answer is yes! A very simplified model of a flush toilet’s nonlinear behavior is as follows: it’s a bucket, into which water can be poured, and there is a hole at height $h \geq 0$. If you pour in volume $v$ of water into the bucket, the output that flows out of the hole is $\text{ReLU}(v - h)$.

The second component we need to build a neural network is a linear map. We can do this by attaching a branching pipe to the hole. This component will have $k$ branches with cross-sectional areas $A_1, A_2, \dots, A_k > 0$. By conservation of mass and a simple pressure argument, the amount of water that pours out of branch $i$ is $A_i / \Sigma_j A_j$.

Together, these components allow us to compute a function from $\mathbb{R}\rightarrow \mathbb{R}^k$, which looks something like $\text{PeLU}(v, \vec{A}, h) = \text{ReLU}(v - h)\cdot \vec{A} / \Sigma_j A_j$. Here, “PeLU” stands for “Porcelain-Emulated Linear Unit.” It is clear how to vectorize this expression over $v$, which effectively creates a new kind of neural network “layer” with trainable parameters $\vec{A}$ and $h$ for each input dimension. To enforce the positivity constraint on $h$ and $A_i$, we will actually work with the following key equation: $\text{PeLU}(v, \vec{A}, h) = \boxed{\text{ReLU}(v - h^2) \cdot \text{softmax}(\vec{A})}$.

All that is left to do at this point is to implement this in PyTorch and train it.

import torch

class PeLU(torch.nn.Module):
    def __init__(self, in_feat, out_feat):
        super().__init__()
        self.heights = torch.nn.Parameter(
            torch.randn(in_feat))
        self.weights = torch.nn.Parameter(
            torch.randn(in_feat, out_feat)
        )

    def forward(self, X):
        X = torch.nn.functional.relu(X - self.heights ** 2)
        X = X.matmul(self.weights.softmax(dim=1))
        return X

Here, I built a PeLU layer that can be slipped into any PyTorch model, mapping in_feat inputs to out_feat outputs. Next, let’s stack some PeLU layers together and train the result on the classic “Iris” dataset, which has 4 features and assigns one of 3 labels. We will create a “hidden layer” of size 3, just to keep things interesting.

from iris import feat, labl

m = torch.nn.Sequential(
    PeLU(4, 3),
    PeLU(3, 3)
)
o = torch.optim.Adam(m.parameters(), lr=0.01)
lf = torch.nn.CrossEntropyLoss()

for i in range(10_000):
    o.zero_grad()
    pred = m(feat * 10)
    loss = lf(pred, labl)
    loss.backward()
    o.step()

print('Loss:', loss)
print('Error:', 1. - ((torch.argmax(pred, dim=1) == labl) * 1.).mean())

This trains very quickly, in seconds, and gives an error of 2%. Of course, we haven’t split the dataset into a train/test set, so may be be overfitting.

By the way, you may have noticed that I multiplied feat by 10 before passing it to the model. Because of the conservation of mass, the total amount of water in the system is constant. But each bucket “loses” some water that accumulates below the hole. To make sure there’s enough water to go around, I boosted the total amount.

But that’s all that needs to be done! Once we export the parameters and write a small visualizer…

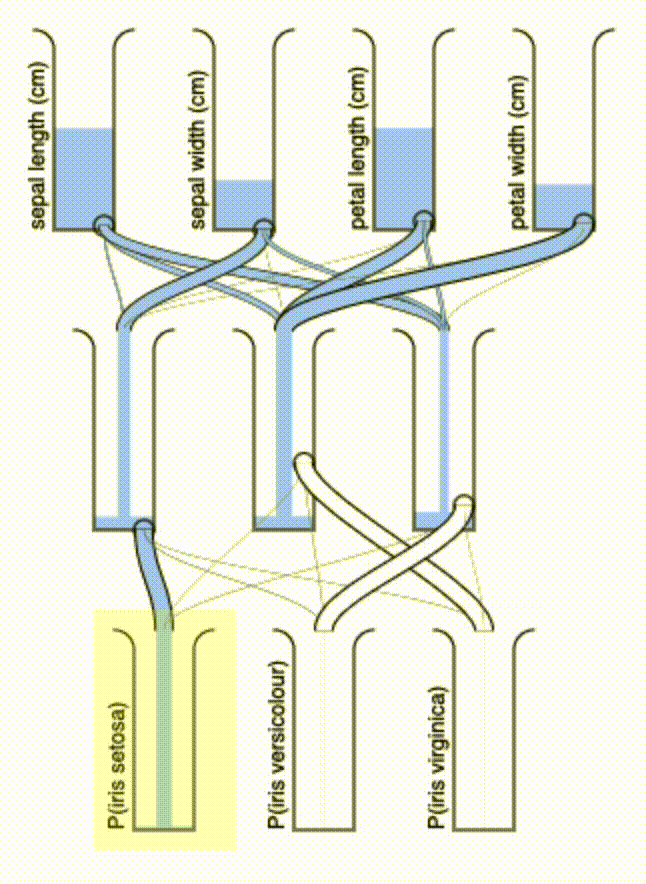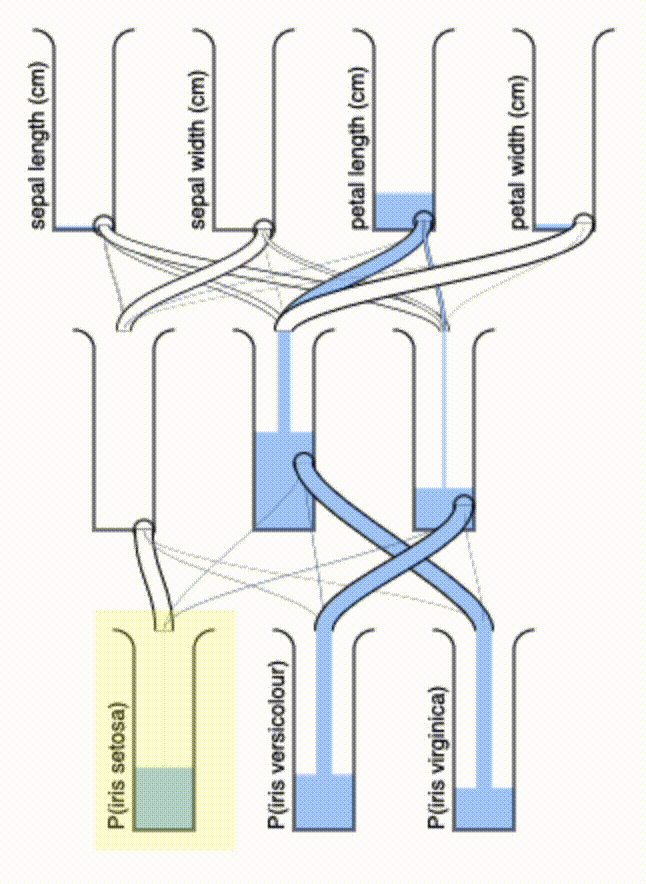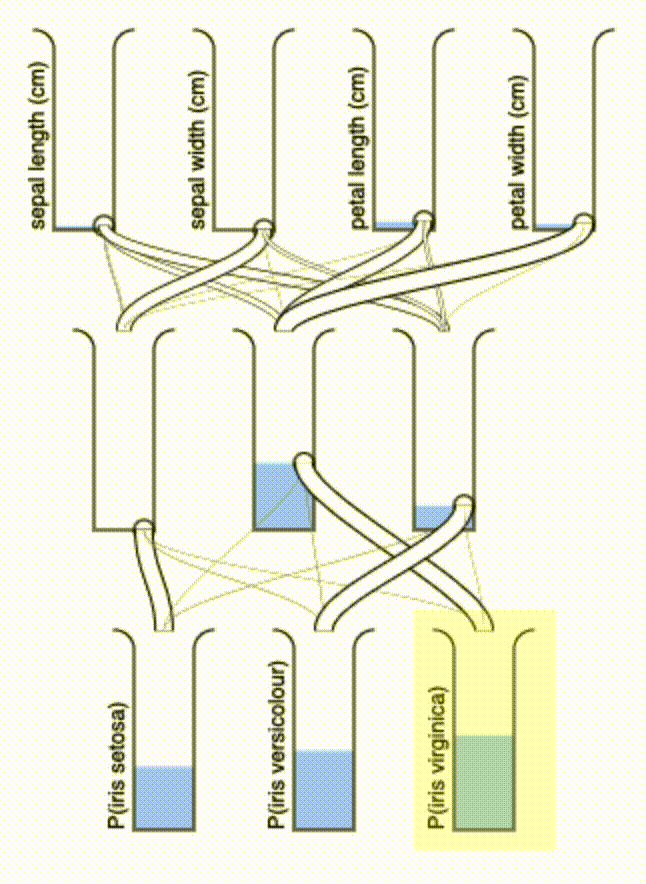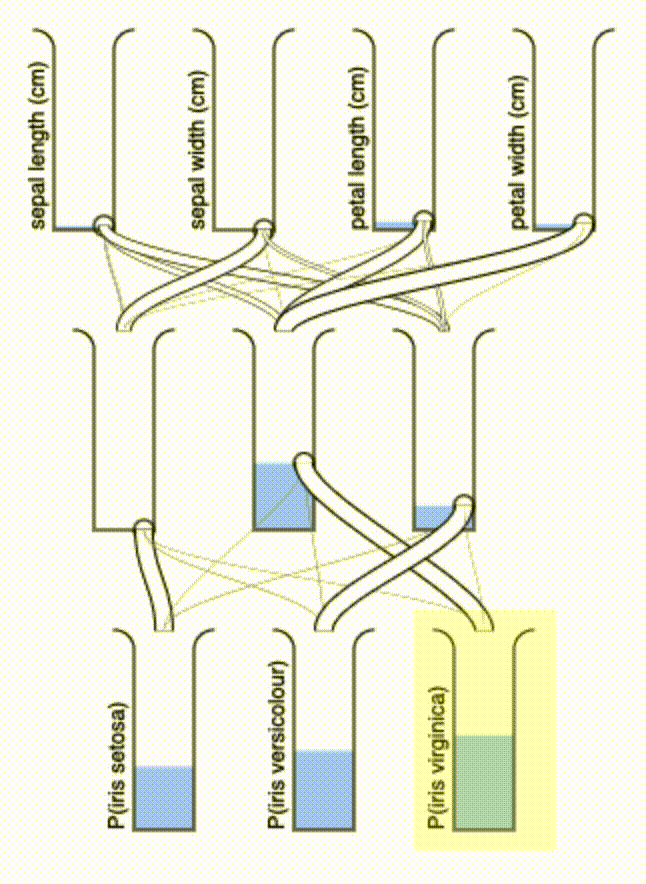
Isn’t that a delight to watch? I may even fabricate one to have as a desk toy — it shouldn’t be hard to make a 3D-printable version of this. If we wanted to minimize the number of pipes, we could add an L1 regularization term that enforces sparsity in the $\vec{A}$ terms.

Some final thoughts: this system has a couple of interesting properties. First, there’s a kind of “quasi-superposition” that it allows for: if you pour in more water on top to incrementally refine your input, the output will automatically update. Second, the “conservation of mass” guarantees that the total water output will never exceed the total water input. Finally, it’s of course entirely passive, powered only by gravity.

This has me wondering if we can build extremely low-power neural network inference devices by optimizing analog systems using gradient descent in this way (a labmate pointed me to this, for example).

Below is a little widget you can use to enjoy playing with PeLU networks. All inputs must be between 0 and 10. :)

Sepal length (cm):
Sepal width (cm):
Petal length (cm):
Petal width (cm):